期权定价模型B-S公式_ETF、期权等金融知识普及专栏_投教基地

期权定价模型B-S公式

发表日期：2019年12月16日

1997年10月10日，第二十九届诺贝尔经济学奖授予了两位美国学者，哈佛商学院教授罗伯特·默顿(RoBert Merton)和斯坦福大学教授迈伦·斯克尔斯(Myron Scholes)。他们创立和发展的布莱克——斯克尔斯期权定价模型(Black Scholes Option Pricing Model)为包括股票、债券、货币、商品在内的新兴衍生金融市场的各种以市价价格变动定价的衍生金融工具的合理定价奠定了基础。

斯克尔斯与他的同事、已故数学家费雪·布莱克(Fischer Black)在70年代初合作研究出了一个期权定价的复杂公式。与此同时，默顿也发现了同样的公式及许多其它有关期权的有用结论。结果，两篇论文几乎同时在不同刊物上发表。所以，布莱克—斯克尔斯定价模型亦可称为布莱克—斯克尔斯—默顿定价模型。默顿扩展了原模型的内涵，使之同样运用于许多其它形式的金融交易。瑞典皇家科学协会(The Royal Swedish Academyof Sciencese)赞誉他们在期权定价方面的研究成果是今后25年经济科学中的最杰出贡献。

(一)B-S模型有7个重要的假设　

1、股票价格行为服从对数正态分布模式；

2、在期权有效期内，无风险利率和金融资产收益变量是恒定的；

3、市场无摩擦，即不存在税收和交易成本，所有证券完全可分割；

4、金融资产在期权有效期内无红利及其它所得(该假设后被放弃)；

5、该期权是欧式期权，即在期权到期前不可实施。

6、不存在无风险套利机会；

7、证券交易是持续的；

8、投资者能够以无风险利率借贷。

(二)荣获诺贝尔经济学奖的B-S定价公式

$说明: \mathbf{C=S\bullet N(d_1)-Le^{-rT}N(d_2)}$ 　

　　其中:

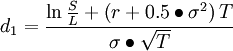
　　 $说明: d_1= \frac {\ln \frac{S}{L} + \left( r+0.5\bullet \sigma^2 \right)T}{\sigma\bullet \sqrt{T}}$

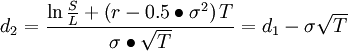
　 $说明: d_2= \frac { \ln \frac{S}{L} + \left( r-0.5\bullet \sigma^2 \right)T}{\sigma\bullet \sqrt{T}}=d_1-\sigma\sqrt{T}$

l C—期权初始合理价格　

l L—期权交割价格

l S—所交易金融资产现价

l T—期权有效期

l r—连续复利计无风险利率

l σ2—年度化方差

l N()—正态分布变量的累积概率分布函数 $说明: \left(\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{d_n} e^{-\frac{x^2}{2}}\, dx\right)$ ，

自B-S模型1973年首次在政治经济杂志(Journal of Political Economy)发表之后，芝加哥期权交易所的交易商们马上意识到它的重要性，很快将B-S模型程序化输入计算机应用于刚刚营业的芝加哥期权交易所。该公式的应用随着计算机、通讯技术的进步而扩展。到今天，该模型以及它的一些变形已被期权交易商、投资银行、金融管理者、保险人等广泛使用。衍生工具的扩展使国际金融市场更富有效率，但也促使全球市场更加易变。新的技术和新的金融工具的创造加强了市场与市场参与者的相互依赖，不仅限于一国之内还涉及他国甚至多国。结果是一个市场或一个国家的波动或金融危机极有可能迅速的传导到其它国家乃至整个世界经济之中。我国金融体制不健全、资本市场不完善，但是随着改革的深入和向国际化靠拢，资本市场将不断发展，汇兑制度日渐完善，企业也将拥有更多的自主权从而面临更大的风险。因此，对规避风险的金融衍生市场的培育是必需的，对衍生市场进行探索也是必要的，我们才刚刚起步。