买卖平价公式对于期权的意义相当于，万有引力定律在力学中的地位一样重要。它不依赖于任何模型，是一个普适的关系。

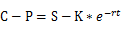
买卖平价关系（Put-call parity）是指一份具有相同的行使价与到期日的认购期权多头与认沽期权空头的投资组合等价于一份标的多头和一个按无风险利率贷出的零息债券空头。

买卖平价关系想要成立的话，是需要有一个前提，那就是在无套利的完备的金融市场条件下。在这个条件下，没有股利支付切其他条件相同时欧式看涨期权和看跌期权之间存在的确定性关系。看涨期权与看跌期权价格有相同的执行价格和到期日，零息债券/纯贴现债券，或者银行存款的到期日也要和期权的到期日一致。

期权平价套利就是捕捉上述等式不成立时的套利机会。在一个高效市场中，所有的市场信息会在第一时间反映在价格上，资产的价格与价值相等。而市场是人的市场，人的非理性交易会使价格产生偏移，这就使套利机会成为可能。该公式不受制于任何期权定价模型的影响而始终保持成立。并且无需考虑波动率因素，可根据其来判断期权价格是否偏离合理价格，从而发现套利机会。

其理论关系成立的逻辑是等式左右两边所代表的资产在期权到期日的收益完全相同，因而在到期日之前的任何一天其价值也应当相同，否则可以在做多低估资产的同时做空高估资产获得无风险收益。

做空看涨期权组合、做多看跌期权组合

当出现 C + Ke ^ {-rT} > P + S 的情况时，看涨期权被高估，因此我们卖出看涨期权，并借入 K e ^ {-rT} 价值的无风险资产，买入低估的看跌期权，同时买入标的资产。

做空看跌期权组合，做多看涨期权组合

当出现 C + K e ^ {-rT} < P + S 的情况时，看跌期权被高估，因此我们卖出高估的看跌期权，同时卖出标的资产，买入低估的看涨期权，同时借出K e ^ {-rT}价值的无风险资产。

在无风险套利时，不可忽视流动性风险与冲击成本。假设交易时都能按对价成交，即买入时按卖一价成交， 卖出时按买一价成交。据测算，最坏情况下，完成一次套利交易，冲击成本接近 0.2%，实际交易中平均冲击成本应该在 0.1% 左右。冲击成本与市场流动性有很大关系，是套利交易的主要交易成本。

综上所述，只有合理高效捕捉交易机会，才能真正实现无风险套利。